Theory of Generalization - 舉一反三定理,是指訓練時餵一筆資料給學習演算法後
它要能夠解決其他三筆類似的資料 : P
當抽樣的N足夠大,且成長函數mH(N)被中斷點給限制住,使得Ein與Eout大約相同的時候
舉一反三定理就能夠成立
圖一、複習
在先前學習筆記17中,已經教過成長函數mH(N)會被限制函數B(N,k)給限制住
而限制函數B(N,k)又會被它自己的最高次項N的k-1次方給限制住
因此,可以得到圖二的不等式結果
圖二、成長函數與限制函數和最高次項的關係
圖三、成長函數複習
配合前一個學習筆記18中說過的VC Bound
圖四、複習VC Bound
我們必須要確保圖五中,mH(N)成長函數會在k的時候中斷指數型增長(好的hypotheses set H)
、抽樣的資料數N夠大(好的資料),使得Eout 大約等於 Ein'
同時學習演算法A選擇了一個好的假設模型g,同時取樣的資料中的Error很小的情況下
我們可以順利的進行學習~
圖五、學習可達成
今天我們介紹一個新的觀念 VC Dimension
VC Dimension 的定義是最大的非break point的資料點 (詳細的證明可以看 [1] )
若 k 是break point發生的資料點個數,則 VC Dimension = k-1
同時,是最多可以被 shatter 的資料點個數
圖六、VC Dimenson
圖七、成長函數與VC Dimension
常見函數的 VC Dimension,如圖八中列出來的所示。
如果今天VC Dimension是有限個的話,會是好的Hypotheses set H
圖八、常見函數的 VC Dimension
好的Hypotheses set H,即 VC Dimension 是有限個的話,能確保 Ein 跟 Eout會很接近
上述的事情跟選擇哪一個學習演算法 A、輸入資料分佈P 以即 目標函數 f 是沒有任何關係的!
圖九、複習整個學習的流程
課後練習
這題我以為是3,但是答案卻是4。因為只有看到手上的N筆資料不能被shatter,但是其他N筆
可以呢? 所以在不確定 VC Dimension究竟是 > N 還是 <N的情形下,我們是不能任意下結論
的!
----------------------------------------------------------------------------------------------------------------
複習兩個主線故事 : P
圖十、2D PLA 複習
N維 Perceptron 的VC Dimension
圖十一、不同Perceptron的VC Dimension
若要證明N維的 Perceptron VC Dimension是 N+1,則需要透過圖十二的兩個步驟來證明
不等式的兩個方向都證明為可行的時候,那麼唯一的交集點就是N+1
圖十二、兩步證明 N維 VC Dimension
Step 1: 證明 dvc ≥ d+1
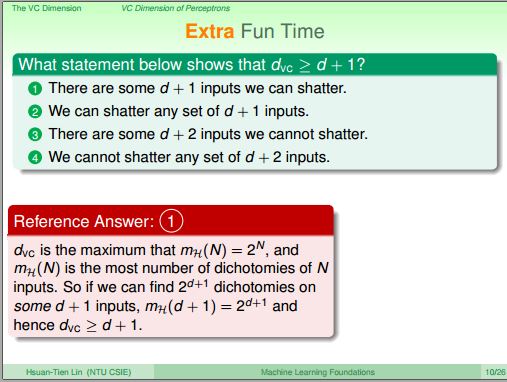
課堂練習
答案為何是1 ?
(此段有點不懂)
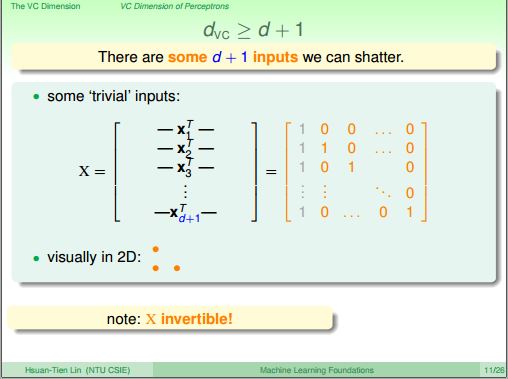
圖十三分享一組特別資料X矩陣,接下來要證明某些 d+1個輸入資料能夠被 shatter
而X的反矩陣是存在的(invertible)
圖十三、X矩陣
圖十四說明一個已知X的反矩陣是存在的
圖十四、X的反矩陣存在
圖十五告訴我們,若要能夠Shatter,則對任意的y來說 sign(Xw) = y 這個式子要能夠成立
圖十五、解釋shatter機制
如圖十六所示,在這邊這個特殊的X矩陣能夠被shatter
圖十六、Step 1 結論
Step 2: 證明 dvc ≤ d+1
前一個問題與這個問題根本差異在哪 ?
證明所有可能性困難度較高,先以下面的圖十七的特殊案例來進行說明
圖十七、X特例分享
圖十八中的 ? 符號實際上在數學上是不存在的
假設前兩項都大於 0,後一項小於0,又因為w相同,xn 是 +1/ -1,則x4 會大於零
圖十八、x4項
所以x4與前幾項是線性相依的關係,如圖十九所示
圖十九、線性相依
那如果是考慮所有資料的一般性的情況呢 ?
把所有資料列在X矩陣中
從圖二十中我們可以看到,X的d+2這項是其它 x項的線性組合
因此會與其他項有線性相依的關係
圖二十、d維度的案例
從反證法的角度來切入,先假設我們可以shatter,產生了某種情形,但是發現無法發生
那麼結果就能被證明是不行的
如果今天我們有一組w,剛好與圖二十一中X的d+2等號後面的係數組合一樣
由於線性相依的關係,所以我們沒有辦法產生所有的Dichotomies,因此與前面說可以shatter
這件事情矛盾了
圖二十一、X的d+2項
所以任何d+2的點都不能被shatter,因此得到圖二十二中的結論
即VC Dimension會小於等於d+1
圖二十二、Step 2 的結論
課後練習
根據前面兩個不等式的證明可以知道,VC Dimension dvc = d+1,這題並不困難
根據前面兩個不等式的證明可以知道,VC Dimension dvc = d+1,這題並不困難
----------------------------------------------------------------------------------------------------------------
[Youtube 影片28 The VC Dimension :: Physical Intuition of VC Dimension @ Machine Learning Foundations]
Degrees of Freedom
從前一節的影片27中,可以將 hypotheses set 中一系列的 w 視作自由度
如圖二十三所表示的圖案,這些許多的 wn (n=0~k-1)可視作能用旋鈕進行調整的參數
如果這些旋鈕是類比式而且可調整的,那麼Hypotheses set H就能夠有無限多種可能
今天如果需要做二元(Binary)的分類,那我們想知道有效的二元自由度是多少
如果wn中有的旋鈕對於決定 dichotomies 沒有幫助,則我們便不需要考慮那項。
至於如何看Hypotheses set夠不夠powerful,也就是我們能夠產生最多的dichotomies
就看它的VC Dimension dvc(H) 是多少
圖二十三、
常見案例的 VC Dimension 分享
Positive Rays中,可以調整的參數(旋鈕)是" a "
Positive Intervals,可以調整的參數(旋鈕)是 " l "、" r "
圖二十四、
VC Dimension代表了Hypotheses的自由度
如圖二十五所示,在前面的課程中有提到學習的兩大問題 :
1. Ein 跟 Eout 是不是很接近 ?
2. Ein是不是夠小 ?
那個時候我們用來量測Hypotheses的自由度是用M
現在我們改用 VC Dimension dvc(H) 這個重要概念來取代M
同時,壞事發生的機率的公式會被修正
如果手上有了資料,在求得 VC Dimension 之後
我們就可以用 VC Dimension 來評估要用哪個學習理論能夠做到最好的效果
圖二十五、
課後練習
其實仔細想的話並不困難。前面已經推出來dvc = d+1,但今天有一個維度的資訊w0被限制住
所以自由度就會是 d+1 減去 1 ,等於d個自由度
----------------------------------------------------------------------------------------------------------------
為了能夠更伸入理解 VC Bound,我們將 VC Bound 的公式重新進行整理
我們將壞事發生的機率訂為 δ,若 P[壞事的機率] ≤ δ
因此,好事發生的機率就是≥ 1 - δ,即 P[好事的機率] ≥ 1 - δ
圖二十六、δ 與霍夫丁不等式
這邊我們可以透過舉一反三的誤差 (Generalization Error)
來知道舉一反三這件事情它做得多好
這邊列出來的雙邊不等式,相當於統計上信賴區間 (Confidence of Interval)
因此,得到Eout的信賴區間
左邊的部分比較不重視,因此用灰色線表示
這邊的Model是指Hypothesis set,model complexity Ω 表示在進行學習時要付出多少代價
圖二十七、信賴區間的概念
將右邊比較重要的不等式部分獨立出來研究
圖二十八、只取右半部的信賴區間
我們針對 Error 還有 VC Dimension 繪製成圖二十九的圖表
(縱軸表示Error,橫軸為VC Dimension)
如圖二十九所示,最好的 VC Dimension 會在中間打星號的地方
從這個結果可以看到,我們不單單只要考慮如何讓 Ein 很小這件事情
還包含了 Model complexity Ω 這項,如果 Ein 越來越小,Ω這個代價函數就會越來越大!
圖二十九、 Error 與 VC Dimension 之間的關係
VC Bound還有另一層含義,
圖三十、再說明公式一次
我們今天以一個例題來進行說明,看看我們 N 帶入越來越多的時候,會發生什麼事情 : P
觀察 N 與 VC Bound 之間的關係,竟然需要 10,000 倍的 VC Bound 個數據,似乎不容易蒐集
因此,實務上,大約 10 倍就夠用了 (10怎麼來的,這邊有點模糊,解釋沒有這麼清楚)
圖三十一、VC Bound 理論與實務量級的差別
理論上需要10,000倍,但是實務上卻只要 10 倍 !? (你沒看錯,就是10而已,差了1,000倍 )
可以發現 VC Bound 在這邊只有寬鬆(Loose)的要求
圖三十二、VC Bound的取樣寬鬆程度
那為什麼能夠只需要用這麼寬鬆的資料個數舊能夠達到學習效果呢 ?
圖三十三中列出了所有的原因
第一點,霍夫丁不等式,對於任何資料分佈與目標函數都適用
第二點,任意資料點都可以
第三點,是使用了上限的上限,而不是成長函數
第四點,聯集 (Union Bound) 包山包海的情況不太可能發生,因此並沒有想像中這麼多
圖三十三、取樣個數寬鬆的四個背後原因
課後練習
掌握了 VC Bound,就掌握了機器學習中最重要的工具 (這麼厲害!?)
總結
在這章介紹了VC Dimension是最大的non-break point,與 VC Dimension 是d維度 + 1
圖三十四、總結
----------------------------------------------------------------------------------------------------------------
[1] VC Dimension : 對岸的網友整理的詳細 VC Dimension 的筆記,看來需要再多加把勁



































沒有留言:
張貼留言