原始的Hypotheses H,如果從Perceptron的資料分類方法來看
無窮多個的Perceptron就有無窮多個分類結果
Ex. 光是2D平面的分類,我可以在任何位置,用任何旋轉角度對資料進行分類
圖一、Perceptron分類示意圖
Dichotomy : 二分法
Dichotomy 指的是資料的二分法
上一個筆記12中有提到,若能從分種類的角度來看的話,可以收斂成為有限種類的可能
圖一、資料點二分分類
找到欲解決問題的成長函數
假設今天有一個二分法分類器能夠將資料點二分成 o (+1) 以及 x (-1)
其中選出最大(max)的 Dichotomies set 當作衡量的依據,取作mH
這個 mH函數 叫作 成長函數 (Growth Function)
mH(N) 就是指資料個數為N的時候,最多分類個數的 Dichotomies set 中的分類個數
未來就是用來取代有限但很可能很大的 hypotheses個數M (學習筆記12有提到M)
而且成長函數的結果是有限的,同時會被2的N次方所限制住
圖二、Growth Function
Growth Function案例分析
Positive Rays
今天如果有一個一維的資料,我們設定一個門檻值(Threshold) a
當如果數據大於a的話,則標記為+1;反之,則為-1
這個相當於一個一維的Perceptron分類問題,最多的可能為 N+1 種(遠小於2的N次方)
右下角就是分類結果的示意圖
圖三、Positive Rays
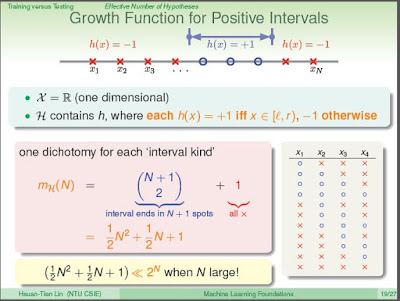
但是,如果是一個區間(Interval)的話,總共有幾種不同的可能?
就相當於N個2種不同物體,作不盡相異物的排列的問題
可以以 C 的 N+1 取 2 (已包含全部都是o的情況)再加上 1(全部都是x的情況)
N+1
mH = ( ) +1 = (N平方 + N)/2 +1 = N平方/2 + N/2 + 1
2
把圖四 mH 的結果給推導出來
一般來說N個資料點,總共有2的N次方種分類可能
若N很大的話,2的N次方所算出來的結果還是可能很大
因此,最終我們推導得到的結果是mH會遠小於 2的N次方
N個數據可能的結果不會非常大,對於我們來說是個好消息!
圖四、Positive Intervals
第三個課本中的例題是如何算成長函數
如果今天我們有ㄧ個凸角(convex),我們就算是+1
圖五、convex hypotheses
如果今天有N的點,我們隨機選取其中的點,而且每個點都可以被計入dichotomies set
所以這個例子的 成長函數 mH 就是 2 的N次方
圖六、convex hypotheses的Growth function
在這個case中,我們可以說這些N個資料點能夠被假設模型 h 打碎
shatter意思是指,這N個資料點的二分法分類,能夠百分百的被假設模型組合 H 實現出來
沒有不能被實現的情況






沒有留言:
張貼留言